W piątym wieku przed naszą erą znany filozof Zenon z Elei usilnie próbował pokazać, że ruch jest jedynie złudzeniem, które nie jest możliwe w rzeczywistości. Zamiast tego przyczynił się do rozwinięcia naszej wiedzy o ciągach nieskończonych. Zobaczmy, czego dziś może nas nauczyć oraz czy Achilles zdoła przegonić żółwia.

Jeden z jego znanych paradoksów został sformułowany następująco:

Achilles i żółw stają na linii startu wyścigu na dowolny, skończony dystans. Achilles potrafi biegać 2 razy szybciej od żółwia i dlatego na starcie pozwala oddalić się żółwiowi o 1/2 całego dystansu. Achilles, jako biegnący 2 razy szybciej od żółwia, dobiegnie do 1/2 dystansu w momencie, gdy żółw dobiegnie do 3/4 dystansu. W momencie gdy Achilles przebiegnie 3/4 dystansu, żółw znowu mu „ucieknie”, pokonując 7/8 dystansu. Gdy Achilles dotrze w to miejsce, żółw znowu będzie od niego o 1/16 dystansu dalej, i tak w nieskończoność. Wniosek: Achilles nigdy nie dogoni żółwia mimo, że biegnie od niego dwa razy szybciej, gdyż zawsze będzie dzieliła ich zmniejszająca się odległość. [Wikipedia]

Z matematycznego punktu widzenia nie jest to trudny problem. Jeśli dystans nazwiemy d, a prędkość żółwia v, lokalizację Achillesa możemy określić następującym wzorem:

$$x = v*2 * t$$

Gdzie t to czas. Tymczasem lokalizację żółwia:

$$x = d/2 + v * t$$

W momencie, w którym Achilles dogoni żółwia, ich x będą równe. Oznacza to więc, że:

$$v*2*t = d/2 + v * t$$

$$t = 2d/v$$

$$x = d$$

Wynika z tego, że Achilles dogoni żółwia. Takie podejście może być jednak traktowane jako małe oszustwo. Nie tak Zenon sformułował problem. Przeanalizujmy go więc jego sposobem. Za pierwszym razem Achilles przebiegł dystans d/2. Następnie d/4, potem d/8, d/16 itd. Wyraźnie widać, że kolejne dystanse są coraz mniejsze i opisane są równaniem (dla n = 0, 1, 2, …):

$$\frac{d}{2^{n}}$$

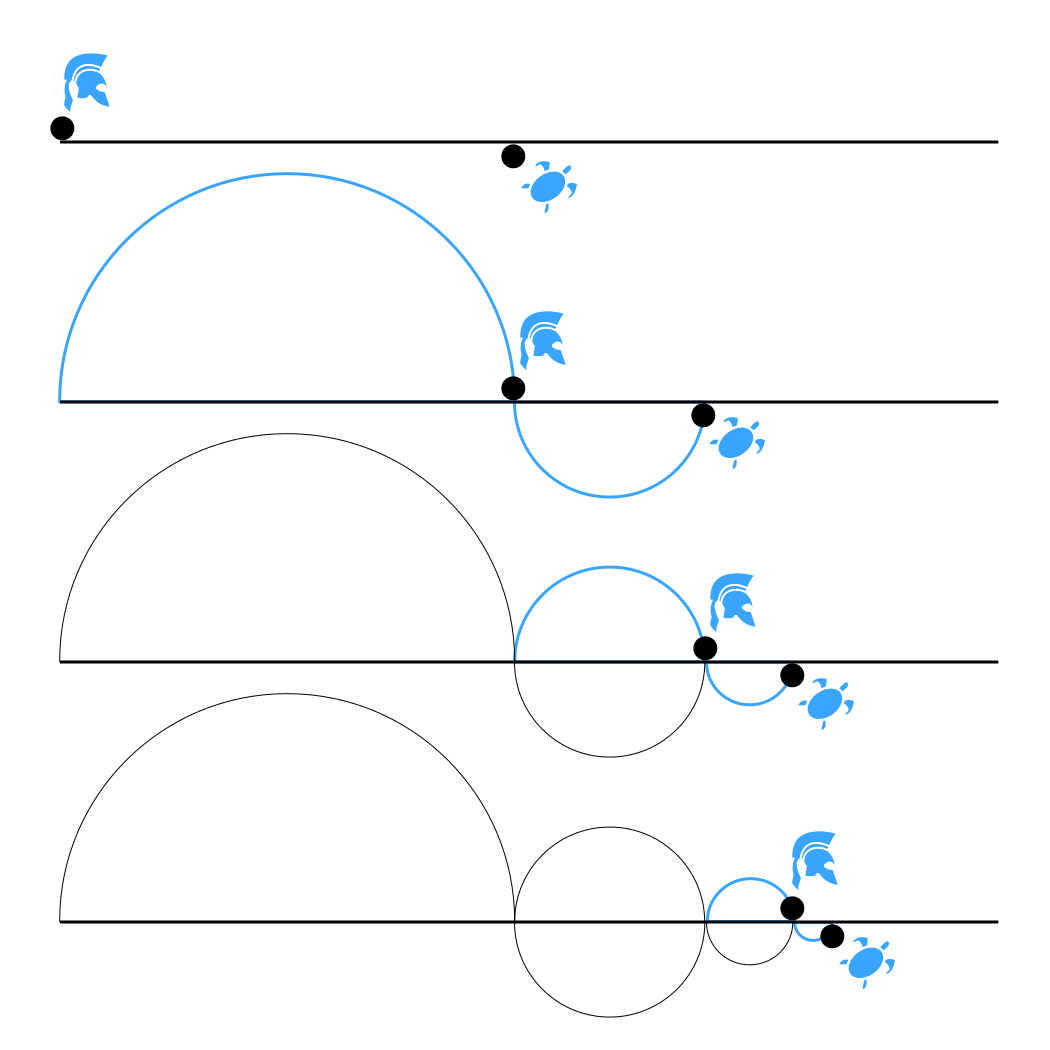
Cały dystans to suma tych dystansów cząstkowych. Ile ich jest? Jak już ustaliliśmy - nieskończoność. Łączny dystans opisany jest więc następującym równaniem:

$$\frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \frac{d}{16} + \frac{d}{2^n} + ... = \sum_{n=1}^{\infty} \frac{d}{2^{n}}$$

Nieskończona liczba fragmentów składa się na tę sumę, wynik jednak nie jest nieskończony. Kolejne części maleją szybciej niż wnoszą one do sumy. Pomyślmy o wyniku relatywnie do d. Jak szybko się do niego przybliżamy? Po pierwszym etapie Achilles przebył 0.5 dystansu. Po drugim 0.75. Po trzecim 0.875, następnie 0.9375, 0.96875, 0.984375 i 0.9921875. Po dziesiątym 0.9990234375. Wyraźnie zbliżamy się do długości dystansu, ale nie możemy go przekroczyć. Po 100 etapie jest to już 30 dziewiątek po przecinku. Jak dużo etapów potrzebujemy, by osiągnąć cały dystans? Odpowiedź to dokładnie nieskończoność.

Sumę tego ciągu można określić wizualnie. Wystarczy, że narysujesz kwadrat, a potem przedzielisz go na dwie równe części. Następnie jedną z tych części podzielisz na kolejne 2 równe części i tak dalej. Mógłbyś dzielić tak w nieskończoność i na koniec uzyskałbyś kwadrat, a w nim kolejne prostokąty, z czego każdy 2 razy mniejszy.

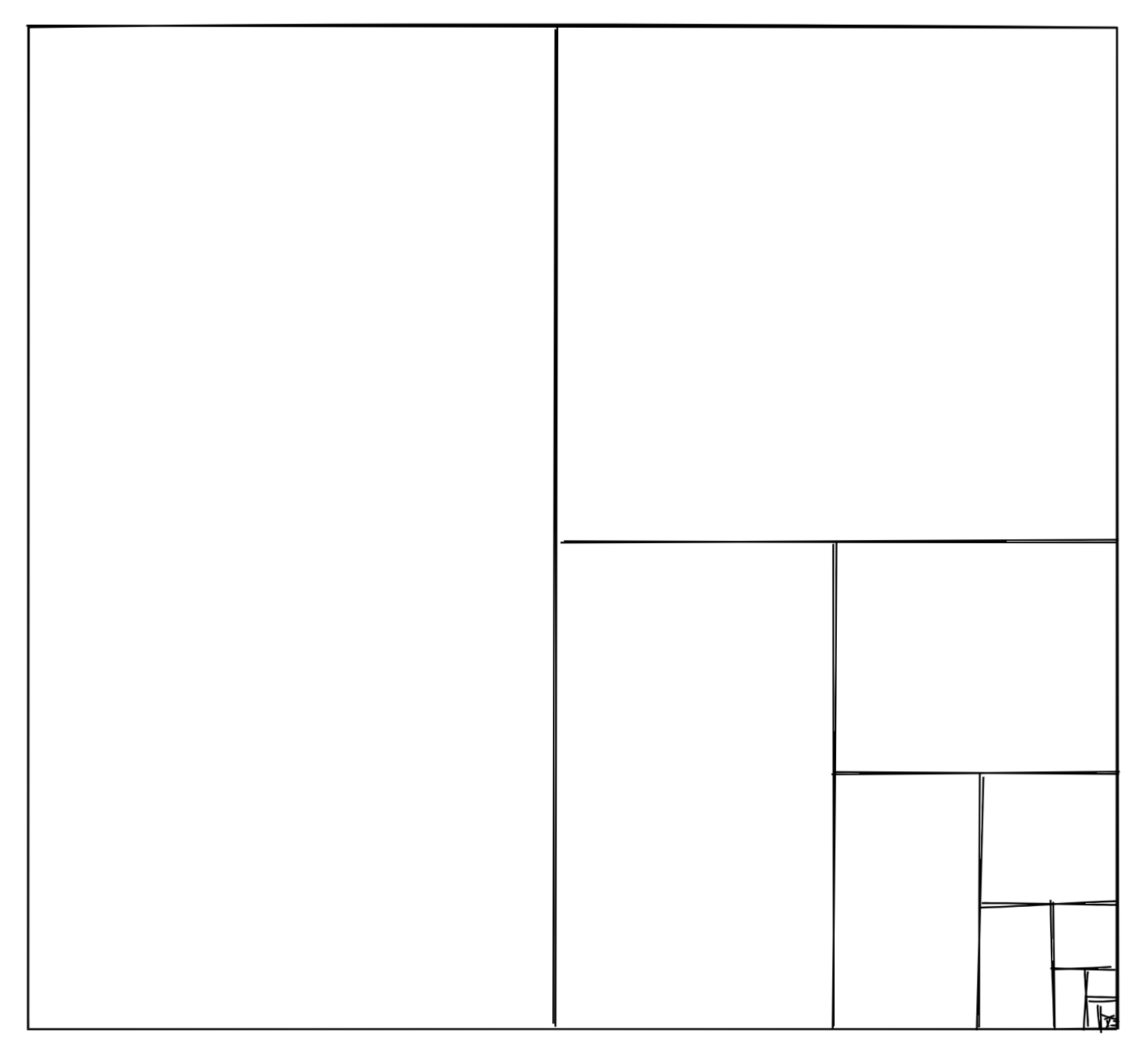
Poprzez taki prosty wizualny dowód wiemy, że ta suma wynosi 1, a więc Achilles dogoni żółwia po dystansie d.

$$\sum_{n=1}^{\infty} \frac{d}{2^{n}} = d$$

Ten przykład jest jednak mało realistyczny. Zakładałbym, że Achilles będzie szybszy od żółwia więcej niż 2 razy. Dla ustalenia uwagi załóżmy, że jest on 10 razy szybszy, a żółw ma przewagę proporcjonalnie taką samą, czyli d/10. W jakim miejscu Achilles go dogoni? Za pierwszym razem przebiegnie on 0.1d, potem 0.01d, potem 0.001d, następnie 0.0001d, 0.00001d, itd. Łatwo się domyślić, że przebiegnięty dystans będzie stanowił 0.11111… d, o czym mówimy 0 i 1 w okresie d, a zapisujemy jako 0.1(1)d.

Wiemy więc w jakim czasie Achilles dogoni żółwia w przypadku, gdy jest od niego 2 razy oraz 10 razy szybszy. Co jednak w innych przypadkach?

Wiemy, że wzór na odległość, po jakiej Achilles dogoni żółwia, jest następujący:

$$\sum_{n=1}^{\infty} \frac{d}{p^{n}} = \frac{d}{p} + \frac{d}{p^2} + \frac{d}{p^3} + ...$$

Gdzie p to o ile razy Achilles jest szybszy od żółwia. Ile wyniesie ta suma? Obliczenie sumy ciągu nieskończonego potrafi być skomplikowane, zazwyczaj jednak pomaga jedna prosta sztuczka - nazwijmy wynik tego sumowania Z.

$$Z = \frac{d}{p} + (\frac{d}{p^2} + \frac{d}{p^3} + ...) = \frac{d}{p} + \frac{1}{p}(\frac{d}{p} + \frac{d}{p^2} + \frac{d}{p^3}) + ... = \frac{d}{p} + \frac{1}{p}Z$$ $$Z = \frac{d}{p} + \frac{1}{p}Z$$ $$Z - \frac{1}{p}Z = \frac{d}{p}$$ $$\frac{p - 1}{p}Z = \frac{d}{p}$$ $$Z = \frac{d}{p - 1}$$

Czy ta formuła jest poprawna? Sprawdźmy. W pierwszym przypadku p wynosiło 2, więc Achilles powinien dogonić żółwia w d. Zgadza się to z poprzednimi wyliczeniami. W drugim przypadku p wynosiło 10. Achilles powinien więc dogonić żółwia po 1/9 d, a więc po 0.1(1)d. Znów formuła się zgadza.

Okazuje się, że zawsze jak tylko Achilles będzie szybszy od żółwia, to będzie go w stanie dogonić. Intuicja więc nie zawiodła, a Zenon z Elei się mylił. Aby rozwiązać jego zagadkę musieliśmy jednak sięgnąć po ciągi nieskończone, ale dzięki temu nauczyliśmy się czegoś nowego.